

It provides a range of plausible values to estimate the effect of interest. For example, for any null hypothesis that the change score is less than 0.7, one would reject it.ĬI kinds of focuses on the alternative hypothesis, the effect of interest. However, a CI can be used to test multiple hypotheses. Using CI for hypothesis testing does not provide the exact p-value. Since this CI does not include 0, we would reject the null hypothesis that the change is 0 at the alpha level 0.05. Based on a pre- and post-test design, we find the confidence interval for the change after training is with the confidence level 0.95. Otherwise, we reject the null hypothesis at the significance level $\alpha$.įor example, suppose we are interested in testing whether a training intervention method is effective or not.
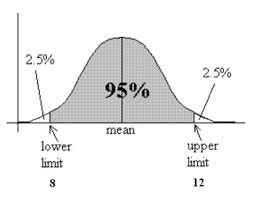
If a corresponding hypothesis test is performed, the confidence level is the complement of respective level of significance, i.e. The desired level of confidence is set by the researchers, not determined by data.When we say, "we are 99% confident that the true value of the parameter is in our confidence interval", we express that 99% of the observed confidence intervals will contain the true value of the parameter. If we conduct many separate data analyses of repeated experiment and each time we calculate a CI, the proportion of such intervals that contain the true value of the parameter matches the confidence level C ($1-\alpha$), This is called confidence level.Therefore, a CI does not necessarily cover the true parameter values at all. For a given CI, it either includes or does not include the population parameter value.Different from the point estimate, a CI consists of a range of potential values as good estimates of the unknown population parameter.Therefore, for two studies on the same topic, the CIs can be very different even following exactly the same study design.
In general, it is different from sample to sample. A CI is an observed interval calculated based on a set of observed data.$l(X)$ and $u(X)$ are called confidence limits (bounds), lower limit and upper limit, respectively. Then $$ is a confidence interval with confidence level $1-\alpha=C$, or $100(1-\alpha)\%$. We can calculate an interval $$ based on the observed data. Assume the observed outcome for $X$ is $x$. Let $\theta$ denote a population parameter (unknowns) and $X$ denote a random variable (e.g., GPA) from which the data can be observed. A confidence interval (CI) is a type of interval estimate, instead of a point estimate, of a population parameter. Its submission guidelines consist of specific guideline on the use of NHST:Įffective January 2014, Psychological Science recommends the use of the "new statistics" - effect sizes, confidence intervals, and meta-analysis - to avoid problems associated with null-hypothesis significance testing (NHST).Ĭonfidence interval provides an alternative method to NHST, which some have argued provides more information on the NHST. Psychological Science is a prestigious journal for psychological research.


 0 kommentar(er)
0 kommentar(er)
